偏微分方程有限差分定价

import numpy as np
import pandas as pd
import scipy.interpolate as spi
import scipy.sparse as sp
import scipy.linalg as sla
import time
from dataclasses import dataclass
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import plotly.graph_objects as go
%matplotlib inline

1 2	import cufflinks as cf cf.go_offline()

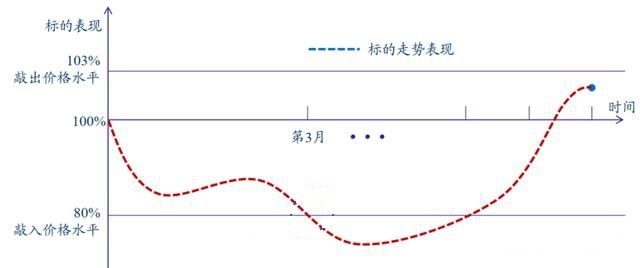
1.雪球自动敲出 (Snowball AutoCallable) 产品

1.1 交易实证

如果长期对某个标的看好，但短期又怕市场变化，可以用雪球结构锁定短期波动。以下标的为中证 500 指数的一个真实雪球结构产品的交易证实 (term sheet) 如下：

产品要素	要素性质（示例）
标的资产	中证 500 指数（000905.SH）
观察期限	360 天，从第三个月开始每月观察敲出+每日观察敲入
期权结构	自动敲入敲出结构
名义本金	100 万
敲出水平	期初价格*103%
敲入水平	期初价格*80%
敲出票息(同红利票息)	25%（年化）
敲出事件（每月观察）	若在任一敲出观察日，挂钩标的收盘价格大于等于敲出水平
敲入事件（每日观察）	若在任一敲入观察日，挂钩标的收盘价格小于敲入水平
收益计算（不包括本金）	敲出（自动提前终止）：25% 名义本金计息天数/365
	未敲入未敲出：25% 名义本金计息天数/365（在此计息天数为 360 天）
	敲入且未敲出（标的期末价格小于期初价格）：(期末价格/期初价格－1) *本金
	敲入且未敲出（标的期末价格处于期初价格与敲出价格之间）：0

名称	数学符号	参数名称
本金	Principal	`Principal`
观察期年限	T	T
期初价格	$S_0$	`S`
敲入水平	$K_{in}$	`KI_Barrier`
敲出水平	$K_{out}$	`KO_Barrier`
敲入价	$K_{in}$	`KI_price`
敲出价	$K_{out}$	`KO_price`
敲出票息	$c_1$	`KO_Coupon`
红利票息	$c_2$	`Bonus_Coupon`
无风险收益率	$r$	`r`
分红	$q$	`div`
波动率	$\sigma$	`sigma`
敲出日	${t_i}$	`T_KO`

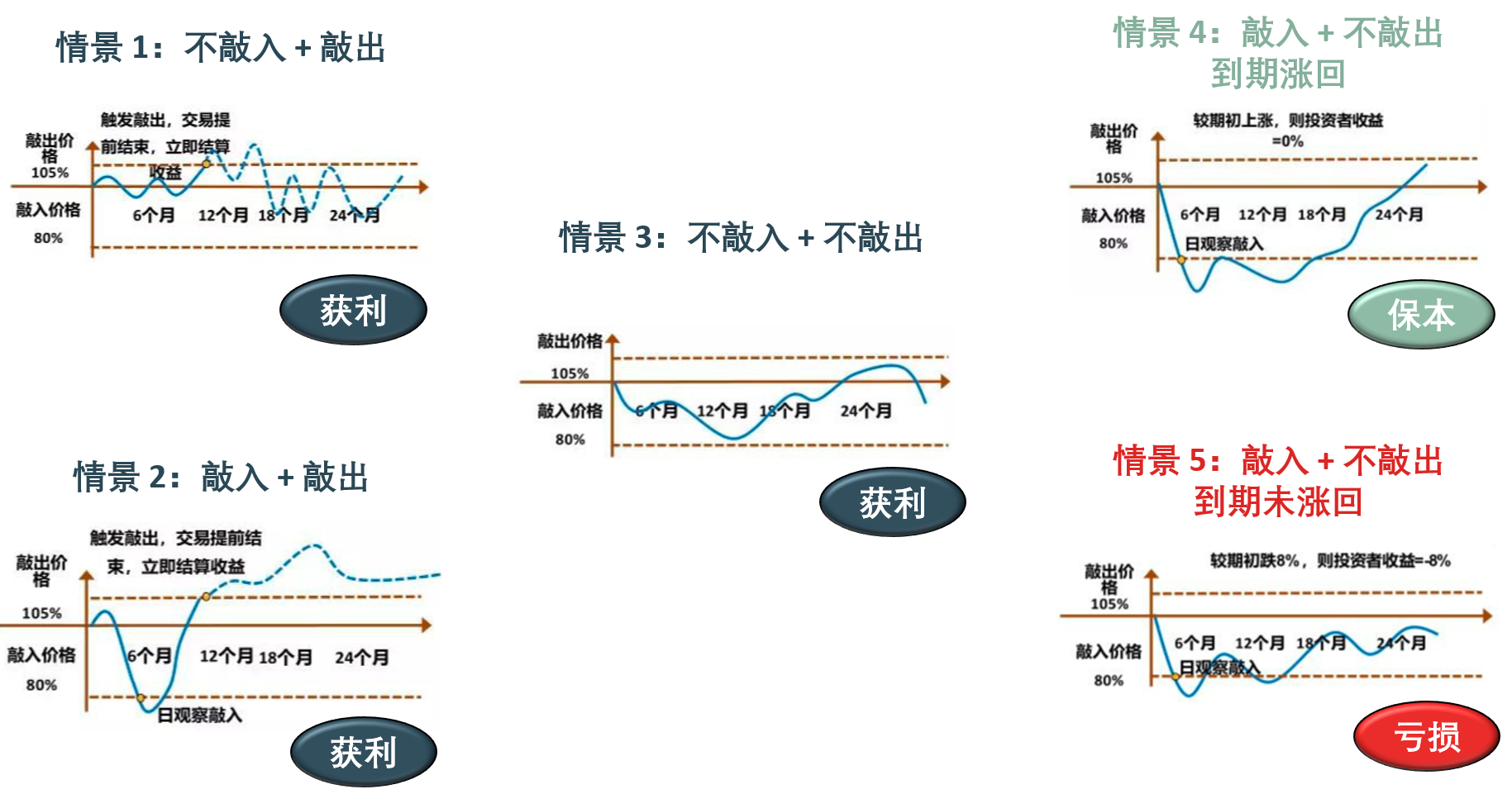
下节分析了雪球结构五种情景收益情况，只有一种情况会亏损，一种会保本，其他三种会获利。

@dataclass
class Snowball_Parameters:
    """parameters to used for pricing snowball option using PDE"""
    
    Principal: float = 10**6                     # principal
    T: int = 1                              # time to maturity in years
    S: float = 6500                              # underlying spot
    St: float = 6500
    KI_Barrier: float = 0.8                  # down in barrier of put
    KO_Barrier: float = 1.03                     # autocall barrier 
    KO_Coupon: float = 0.25                   # autocall coupon (p.a.)
    Bonus_Coupon: float = 0.25                # bonus coupon (p.a.)
    r: float = 0.03                           # risk-free interest rate
    div: float = 0                         # dividend rate
    sigma: float = 0.2455                           # volatility    
    Ns: int = 500                              # number of steps of uly in the scheme
    Nt: int = 365                            # number of discrete time points for whole tenor
    T_KO: np.ndarray = np.arange(30*3/365,30*12.1/365,30/365) # time of knock_out

    
    @property
    def KI_price(self):
        return self.S * self.KI_Barrier
    
    @property
    def KO_price(self):
        return self.S * self.KO_Barrier
    
    @property
    def dt(self):
        return self.T / self.Nt
    
    @property
    def Tvec(self):                 # time axis of grid
        return np.linspace(0, self.T, self.Nt+1) 
    
    @property
    def tau(self):
        return self.Tvec[-1]-self.Tvec
    
    
    def print_parameters(self):
        """print parameters"""
        
        print( "---------------------------------------------" )
        print( "Pricing a Snowball option using PDE" )
        print( "---------------------------------------------" )
        print( "Parameters of Snowball Option Pricer:" )
        print( "---------------------------------------------" )
        print( "Years Until Expiration = ",     self.T )
        print( "Principal = ",                     self.Principal )
        print( "Underlying Asset Price = ",     self.S )
        print( "Knock-in Barrier = ",           self.KI_Barrier )  
        print( "Autocall Barrier = ",           self.KO_Barrier ) 
        print( "Knock-in Price = ",           self.KI_price )  
        print( "Autocall Price = ",           self.KO_price ) 
        print( "Autocall Coupon = ",            self.KO_Coupon )
        print( "Bonus Coupon = ",               self.Bonus_Coupon )
        print( "Risk-Free Rate =",              self.r )
        print( "Dividend Rate =",               self.div )
        print( "Volatility = ",                 self.sigma )
        print( "Discrete underlying points =",        self.Ns )
        print( "Discrete time points =",        self.Nt )
        print( "Time-Step = ",                  self.dt )
        print( "Knock-in Price = ",                  self.KI_price )
        print( "Knock-out Price = ",                  self.KO_price )
        print( "Knock out time = ",                  self.T_KO)
        print( "---------------------------------------------" )

1.2 情景分析

根据上面雪球产品的条款，可粗分为三种情景或细分为 5 种情景，先展示细分过程以及每种情景对应的收益或损失。

snowball scenario

名称	期初价格	上界	下界	敲出收益(%)	红利收益(%)	标的价格	到期价格
数学符号	$S_0$	$K_{out}$	$K_{in}$	$R_1$	$R_2$	$S_t$	$S_T$
参数名称	$S_0$	$K_{out}$	$K_{in}$	$R_1$	$R_2$	$S_t$	$S_T$

从定价的角度来讲，上图的五种情景可以合并成三种：

情景一：合并情景 1 和 2

到期日内观察日标的价格 $St$ 超过了上界 $K{out}$，即发生敲出。这种情况下产品提前结束，
$收益率 = c_1\times\frac{\text{存续月数}}{12}$

情景二：情景 3

标的价格 $St$ 一直在 $[K{in},K_{out}]$ 范围内，未发生触碰上下两条边界，
$收益率 = c_2$

情景三：合并情景 4 和 5

到期日内观察日标的价格 $St$ 跌破了 $K{in}$，到期的时候又回到了期初价格 $S0$ 之上，但是没有触碰 $K{out}$，那么投资者拿回自己的本金。

到期日内观察日标的价格 $St$ 跌破了 $K{in}$，而且到期的时候还在期初价格 $S0$ 之下，但是没有触碰 $K{out}$，那就要承担本金亏损了。

合并起来收益率可写成
$收益率 = \text{min}\left(\frac{S_T-S_0}{S_0}, 0\right)=-\text{max}\left(\frac{S_0-S_T}{S_0}, 0\right)=-\frac{1}{S_0}\text{max}\left(S_0-S_T, 0\right)$

有限差分法

有限差分法（Finite Difference）是求解低维微分方程的常用方法，它的主要思想是通过差分来近似导数，从而找到微分方程的近似解。在 Black-Scholes框架下，我们假设资产 $S$ 服从几何布朗运动，若有一个挂钩 $S$ 的期权，其在 $S$ 时刻的价值可表示为标的 $S$ 价格和时间 $t$ 的函数 $f(t,S)$，则期权价值函数服从如下 BS 微分方程：

$\frac{\partial f}{\partial t}+r S \frac{\partial f}{\partial S}+\frac{1}{2} \sigma^2 S^2 \frac{\partial^2 f}{\partial S^2}=r f,$

其中$r$表示无风险收益率， $\sigma$表示标的波动率。

我们的求解目标是获得时刻 0 时，不同标的价格下期权的价值函数 $f (0, S )$ 。注意到上式对所有价值仅依赖于 $t$ 和 $S$ 的期权均成立，比如欧式看涨、看跌或者二元期权等等，对不同支付结构期权的定价是通过设定不同的边界和终值条件而实现的。

简单的例子——欧式看涨期权

定义数学符号与参数名称：

名称	数学符号	参数名称
观察期年限	$T$	`T`
时间单位	$\Delta t$	`dt`
标的1格	$\Delta S$	`dS`
标的价格上边界	$S_{\max}$	`Smax`
标的价格下边界	$S_{\min}$	`Smin`
时间总数	$N$	`Nt`
标的价格总数	$M$	`Ns`

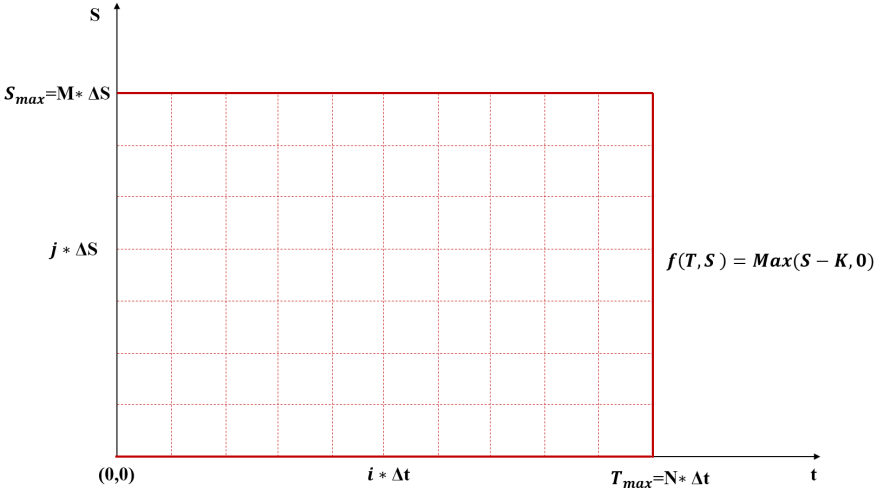
问题陈述

假设到期日为 $T$，行权价为 $K$。

终值条件: $f(T,S) = \max(S-K,0)$
边界条件: $\left\{\begin{array}{l} f\left(t, S_{\max }\right)=S_{\max }-K e^{-r(T-t)}, \quad 0 \leq t \leq T \\ f(t, 0)=0, \quad 0 \leq t \leq T. \end{array}\right.$
其中 $ S_{\max}$ 是一个远大于 $K$ 的常数，是方程在空间维度的上边界。0 是方程在空间维度的下边界。

为了通过有限差分方法求解 $f (0, S )$ ，我们需要先对定义域划分网格，然后使用差分来近似导数，从而将等式 (1) 转化为不同网格点间的线性关系等式。我们将时间维度上区间 $[0,T]$ 等距划分为 $N$ 段，间隔为 $\Delta t$ 。将空间维度的区间 $[0, S_{\max}]$ 划分为 $M$ 段，间隔为 $\Delta S$ 。即网格中的每个点都可表示为 $[ i \times \Delta t , j \times \Delta S ]$，其中 $0\leq i\leq N$，$0,\leq j \leq M$。
欧式看涨期权

有限差分方法——求解微分

根据差分方式的不同，有限差分法可分为显式、隐式和半隐式方法。这些方法的区别在于找到了不同相邻格点之间的线性关系。我们用符号 $f_{i,j}$ 表示 $f(i\Delta t,j\Delta S)$ 。

显式、隐式和半隐式有限差分格式示意图

由于半隐式方法更加稳定，收敛速度也更快，我们这里具体介绍半隐式差分格式的推导与使用。我们用以下有限差分来近似方程 (1) 中的偏导数：

（TODO: 需要做的把显示和隐示也解释清楚，看看能不能用到实战）

$\begin{aligned} & \frac{\partial f}{\partial t} \approx \frac{f_{i+1, j}-f_{i, j}}{\Delta t} \\ & \frac{\partial f}{\partial S} \approx \frac{1}{2}\left(\frac{f_{i+1, j+1}-f_{i+1, j-1}}{2 \Delta S}+\frac{f_{i, j+1}-f_{i, j-1}}{2 \Delta S}\right) \\ & \frac{\partial^2 f}{\partial S^2} \approx \frac{1}{2}\left(\frac{f_{i+1, j+1}+f_{i+1, j-1}-2 f_{i+1, j}}{\Delta S^2}+\frac{f_{i, j+1}+f_{i, j-1}-2 f_{i, j}}{\Delta S^2}\right) \end{aligned}$

代入到方程 (1) 中可得：

$\begin{aligned} \frac{f_{i+1, j}-f_{i, j}}{\Delta t}= & -\frac{r j \Delta S}{2}\left(\frac{f_{i+1, j+1}-f_{i+1, j-1}}{2 \Delta S}+\frac{f_{i, j+1}-f_{i, j-1}}{2 \Delta S}\right) \\ & -\frac{1}{4} \sigma^2 j^2(\Delta S)^2\left(\frac{f_{i+1, j+1}+f_{i+1, j-1}-2 f_{i+1, j}}{\Delta S^2}+\frac{f_{i, j+1}+f_{i, j-1}-2 f_{i, j}}{\Delta S^2}\right) \\ & +\frac{r}{2}\left(f_{i+1, j}+f_{i, j}\right) \end{aligned}$

化简可得共 $M-1$ 个等式：

$\begin{aligned} & -\alpha_1 f_{i,0}\quad\quad+(1-\beta_1) f_{i,1}\quad\quad\quad-\gamma_1 f_{i,2}\quad\quad = \alpha_1 f_{i+1,0}\quad\quad+(1+\beta_1) f_{i+1,1}\quad\quad\quad-\gamma_2 f_{i+1,2} \\ & -\alpha_2 f_{i,1}\quad\quad+(1-\beta_2) f_{i,2}\quad\quad\quad-\gamma_2 f_{i,3}\quad\quad = \alpha_2 f_{i+1,1}\quad\quad+(1+\beta_2) f_{i+1,2}\quad\quad\quad-\gamma_3 f_{i+1,3} \\ &\ldots \\ & -\alpha_j f_{i,j-1}\quad\quad+(1-\beta_j) f_{i,j}\quad\quad\quad-\gamma_j f_{i,j+1} = \alpha_j f_{i+1,j-1}\quad\quad+(1+\beta_j) f_{i+1,j}\quad\quad\quad-\gamma_j f_{i+1,j+1} \\ &\ldots \\ & -\alpha_{M-1} f_{i,M-2}+(1-\beta_{M-1}) f_{i,M-1}-\gamma_{M-1} f_{i,M} = \alpha_{M-1} f_{i+1,M-2}+(1+\beta_{M-1}) f_{i+1,{M-1}}-\gamma_{M-1} f_{i+1,M} \\ \end{aligned}$

其中

$\begin{aligned} &\alpha_j = \frac{\Delta t}{4} (\sigma^2 j^2 -rj)\\ &\beta_j = -\frac{\Delta t}{2} (\sigma^2 j^2 +r)\\ &\gamma_j = \frac{\Delta t}{4} (\sigma^2 j^2 + rj)\\ \end{aligned}$

进一步，可以将等式 (2)写成矩阵形式：

$\mathbf{M}_1 \boldsymbol{f}_i = \mathbf{M}_2 \boldsymbol{f}_{i+1} +\boldsymbol{b}$

其中矩阵 $\mathbf{M}1, \mathbf{M}{2} \in \mathbb{R}^{(M-1) \times (M-1)}$:

$\mathbf{M}_1 = \begin{bmatrix} 1-\beta_1 & -\gamma_1 & 0 & \cdots &0 &0 \\ -\alpha_2 & 1-\beta_2 & -\gamma_2 & \cdots &0 &0 \\ 0 & -\alpha_3 & 1-\beta_3 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & 1-\beta_{M-2} & -\gamma_{M-2} \\ 0 & 0 &0 &\cdots & -\alpha_{M-1} &1-\beta_{M-1} \\ \end{bmatrix}$ $\mathbf{M}_2 = \begin{bmatrix} 1+\beta_1 & \gamma_1 & 0 & \cdots &0 &0 \\ \alpha_2 & 1+\beta_2 & \gamma_2 & \cdots &0 &0 \\ 0 & \alpha_3 & 1+\beta_3 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & 1+\beta_{M-2} & \gamma_{M-2} \\ 0 & 0 &0 &\cdots & \alpha_{M-1} &1+\beta_{M-1} \\ \end{bmatrix}$

其中向量 $\mathbf{f}i, \mathbf{f}{i+1}, \mathbf{b} \in \mathbb{R}^{M-1}$:

$\begin{aligned} &\mathbf{f}_i = [f_{i,1},f_{i,2},\ldots,f_{i,M-1}]^\top\\ &\mathbf{b}_i = [\alpha_1(f_{i,0}+f_{i+1,0}),0,\ldots,0,\gamma_{M-1}(f_{i,M}+f_{i+1,M})]^\top\\ \end{aligned}$

等式 (3) 给出了一个向量迭代等式，我们从终值 $\boldsymbol{f}{N+1}$ 出发向前逐步迭代，最终得到 $\boldsymbol{f}{0}$ ，即期权在期初的价格向量。

LU分解法

注意此步骤通过 scipy 可直接得出，下面仅做理解

LU分解法

我们可以重构等式 (3) 为

$\mathbf{M}_1 \boldsymbol{f} = Q$

其中 $\boldsymbol{f}:=\boldsymbol{f}{i}$， $\boldsymbol{Q}:=\mathbf{M}_2\boldsymbol{f}{i+1} + \boldsymbol{b}$ 均为 $M-1$ 维向量。注意向量 $\boldsymbol{Q}$ 包含时间步骤 $i+1$ 的上一步期权值数组（已知）和边界条件的信息（$\boldsymbol{b}$）。

由于 $\mathbf{M}_1$ 是 tridiagonal 的直接可以分解为其他两个矩阵的乘积 (LU分解)，一个对角和子对角线上非零的矩阵 $\mathbf{L}$，另一个沿对角和超对角线非零的矩阵 $\mathbf{U}$。如下所示

$\mathbf{M}_1 = \begin{bmatrix} 1-\beta_1 & -\gamma_1 & 0 & \cdots &0 &0 \\ -\alpha_2 & 1-\beta_2 & -\gamma_2 & \cdots &0 &0 \\ 0 & -\alpha_3 & 1-\beta_3 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & 1-\beta_{M-2} & -\gamma_{M-2} \\ 0 & 0 &0 &\cdots & -\alpha_{M-1} &1-\beta_{M-1} \\ \end{bmatrix}$ $= \mathbf{L}\mathbf{U} = \begin{bmatrix} 1 & 0 & 0 & \cdots &0 &0 \\ l_2 & 1 & 0 & \cdots &0 &0 \\ 0 & l_3 & 1 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & 1 & 0 \\ 0 & 0 &0 &\cdots & l_{M-1} &1 \\ \end{bmatrix} \begin{bmatrix} d_1 & u_1 & 0 & \cdots &0 &0 \\ 0 & d_2 & u_2 & \cdots &0 &0 \\ 0 & 0 & d_3 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & d_{M-2} & u_{M-2} \\ 0 & 0 &0 &\cdots & 0 &d_{M-1} \\ \end{bmatrix}$

显然 $d_1 = 1-\beta_1$，然后可得对任意 $j \in [2,M-1] \cap \mathbb{N}^+$，有

$\begin{aligned} &u_{j-1} = -\gamma_{j-1}\\ &d_{j} = 1-\beta_j-l_j u_{j-1}\\ &l_j d_{j-1} = -\alpha_j\\ \end{aligned}$

LU迭代步骤分析

现在我们利用分解来求解原始矩阵方程 (4)，首先我们为了符号简便，我们改成如下方程。我们的目标是解出 $\boldsymbol{f} $，LU分解后的方程形式也展示如下：

$\begin{align} \mathbf{M}_1 \boldsymbol{f} &= \boldsymbol{Q}\tag{5} \\ \mathbf{L} \mathbf{U} \boldsymbol{f} &= \boldsymbol{Q} \tag{6}\\ \mathbf{L} \boldsymbol{w} &= \boldsymbol{Q}\tag{7}\\ \end{align}$

其中 $\boldsymbol{f}:=\boldsymbol{f}{i}$， $\boldsymbol{Q}:=\mathbf{M}_2\boldsymbol{f}{i+1} + \boldsymbol{b}$ 和 $\boldsymbol{w}=\mathbf{U} \boldsymbol{f}$ 均为 $M-1$ 维向量。

为了方便理解，再将矩阵代入：

$\mathbf{L} \boldsymbol{w}=\boldsymbol{q} \quad \Longrightarrow \quad \begin{bmatrix} 1 & 0 & 0 & \cdots &0 &0 \\ l_2 & 1 & 0 & \cdots &0 &0 \\ 0 & l_3 & 1 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & 1 & 0 \\ 0 & 0 &0 &\cdots & l_{M-1} &1 \\ \end{bmatrix} \begin{bmatrix} w_1 \\ w_2\\ w_3 \\ \vdots \\ w_{M-2} \\ w_{M-1} \\ \end{bmatrix}= \begin{bmatrix} q_1 \\ q_2\\ q_3 \\ \vdots \\ q_{M-2} \\ q_{M-1} \\ \end{bmatrix}$ $\mathbf{U} \boldsymbol{f} = \boldsymbol{w} \quad \Longrightarrow \quad \begin{bmatrix} d_1 & u_1 & 0 & \cdots &0 &0 \\ 0 & d_2 & u_2 & \cdots &0 &0 \\ 0 & 0 & d_3 & \cdots &0 &0 \\ \vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\ 0 & 0 &0 &\cdots & d_{M-2} & u_{M-2} \\ 0 & 0 &0 &\cdots & 0 &d_{M-1} \\ \end{bmatrix} \begin{bmatrix} f_1 \\ f_2\\ f_3 \\ \vdots \\ f_{M-2} \\ f_{M-1} \\ \end{bmatrix}= \begin{bmatrix} w_1 \\ w_2\\ w_3 \\ \vdots \\ w_{M-2} \\ w_{M-1} \\ \end{bmatrix}$

通过迭代来解出 $\boldsymbol{f}$，迭代核心思想是先解 $\boldsymbol{w}$，然后通过 $\boldsymbol{w}=\mathbf{U} \boldsymbol{f}$ 求解。

我们来看下向量 $\boldsymbol{w}$ 如何迭代的：(正序)

注意 $w_1 = q_1$
$wj = q_j- w{j-1} l_{j}$ for $2\le j \le M-1$

再来看 $\boldsymbol{f}$ 如何迭代的： (倒序)

注意由第 $M-1$ 行可以推出 $f{M-1} = w{M-1} d_{M-1}^{-1}$
$f{j} = (w_j - u{j}f{j+1}) d{j}^{-1} $ for $ M-2 \ge j \ge 1$

LU优势与劣势

优势：

快
如果矩阵 $\mathbf{M}_1$ 与时间无关，分解只需要进行一次

缺点：

不能直接应用于美式期权
如果矩阵 $\mathbf{M}_1$ 依赖于时间，则每个时间步骤都必须进行分解

雪球产品价值

雪球产品可以分解为若干障碍期权的组合，这意味着我们可以先对分解后的多个障碍期权定价，然后加总得到雪球产品价值。

情景1: 敲出

这种情况的payoff可以认为是一个上涨生效触碰期权(One-Touch Up,OTU)。若在到期日T内观察日的标的价格$St \geq K{out}$，则产品自动赎回，$收益率 = c_1\times\frac{\text{存续月数}}{12}$。

$V_1 = OTU\left(R = \left[\frac{3c_1}{12},\frac{4c_1}{12},\ldots,\frac{12c_1}{12}\right]\right)$

其中 $R_1$是敲出票息。

NOTE: 障碍是离散的，且敲出收益依赖于敲出时间。

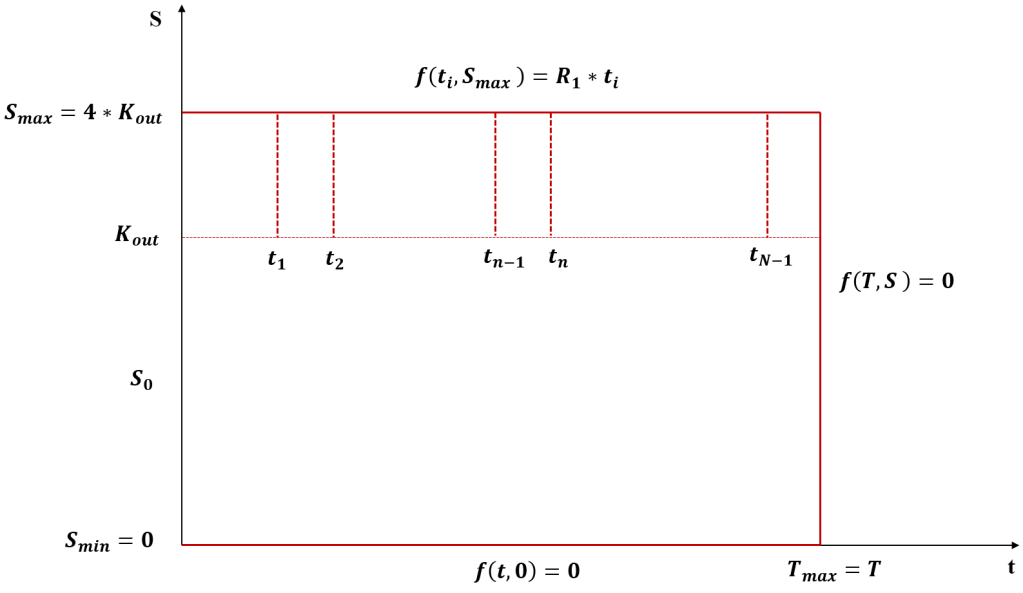
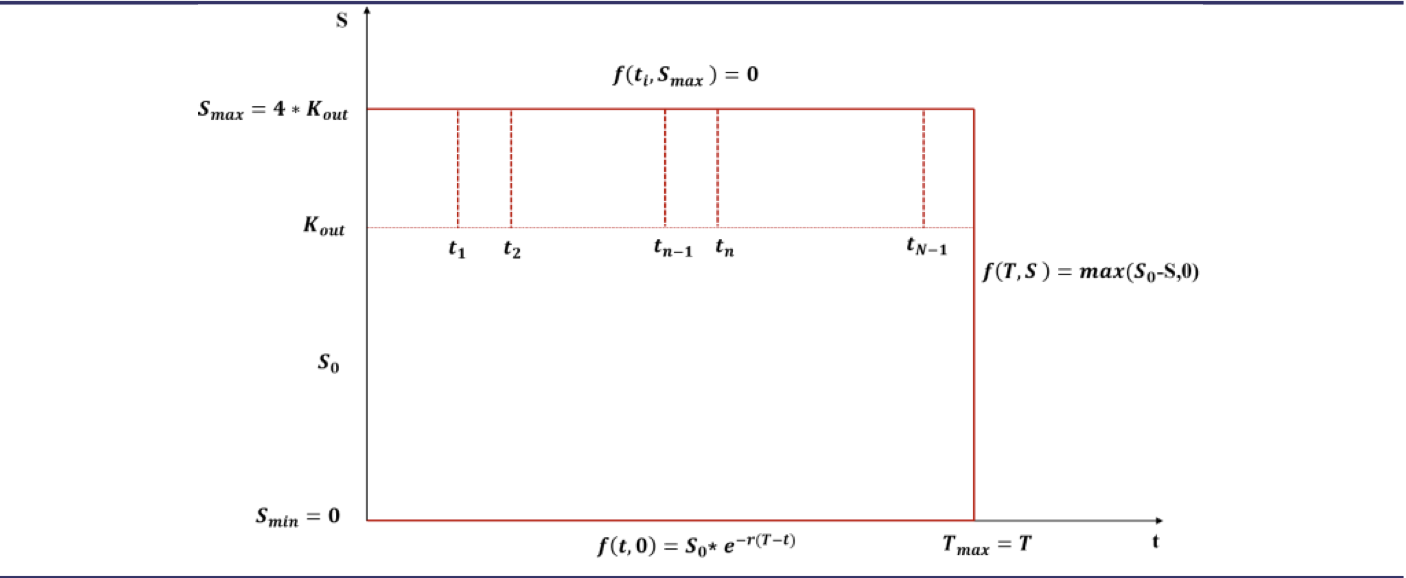
我们首先给出此 OTU 期权价格函数满足的 PDE 示意图，图中给出了方程的边界和终值条件。其中方程下边界为 $S=0$，在下边界的函数值为 $0$；上边界为一个远大于 $S0$ 的数，这里设定为 $4$ (S_max_rate) 倍的敲出价格 $K{out}$ ，上边界处各个观察日 $t_i$ 函数值等于敲出收益

$R_1 \times t_i$

方程终值条件为 $f(T,S)=0$。

上涨生效触碰期权 PDE 示意图

终值条件: $f(T,S) = 0$
边界条件: $\left\{\begin{array}{l} f\left(t_i, S_{\max }\right)=c_1 * t_i, \quad t_1 \leq t_i \leq t_{N-1}\\ f(t, 0)=0, \quad 0 \leq t \leq T. \end{array}\right.$
其中上边界远大于 $S0$ 的数，这里设定为 $4$ (S_max_rate) 倍的敲出价格 $K{out}$ 。0 是方程在空间维度的下边界。

class Snowball_One_Touch_Up(Snowball_Parameters):
    '''
    payoff in the case when knock_out
    '''
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.Smax = 4 * self.KO_price
        self.Smin = 0
        self.dS =  (self.Smax-self.Smin)/self.Ns
        self.Svec = np.linspace(self.Smin, self.Smax, self.Ns+1)
        self.grid = np.zeros(shape=(self.Ns+1, self.Nt+1))
        self.Return_vec = self.KO_Coupon * self.T_KO
        
        
    def _set_terminal_condition_(self):
        pass
    
    def _set_boundary_condition_(self): 
        # discrete barrier with multiple rebates
        f = spi.interp1d(self.T_KO, self.Return_vec, kind='next', bounds_error=False, fill_value=(self.Return_vec[0],self.Return_vec[-1]))
        # upper bound at non-knock-out point
        self.grid[-1, :] = f(self.Tvec) #* np.exp(-self.r*self.tau)

    def _set_coefficient_(self):
        drift = (self.r-self.div)*self.Svec[1:-1]/self.dS
        diffusion_square = (self.sigma*self.Svec[1:-1]/self.dS)**2
        
        self.l = 1/4*(diffusion_square - drift)
        self.c = 1/2*(-diffusion_square - self.r)
        self.u = 1/4*(diffusion_square + drift)

        self.A = sp.diags([self.l[1:], self.c, self.u[:-1]], [-1, 0, 1],  format='csc')
        self.I = sp.eye(self.Ns-1)
        self.M1 = self.I - self.dt*self.A
        self.M2 = self.I + self.dt*self.A
        
    def _solve_(self):
        _, M_lower, M_upper = sla.lu(self.M1.toarray())
        
        #* 1.set boundary condition at T_KO
        KO_idx = np.searchsorted(self.Tvec, self.T_KO)
        update_bool_idx =  (self.Svec>=self.KO_price)
        rbt = self.Return_vec #* np.exp(-self.r*self.tau)
        # 
        for i in reversed(np.arange(self.Nt)):
            
            #* 2.set boundary condition at T_KO
            if i+1 in KO_idx:
                k = np.where(KO_idx==i+1)[0]
                self.grid[update_bool_idx, i+1] = rbt[k]  

            Q = self.M2.dot(self.grid[1:-1, i+1])
            
            Q[0] += self.l[0]*(self.dt*self.grid[0, i] +self.dt*self.grid[0, i+1] )
            Q[-1] += self.u[-1]*(self.dt*self.grid[-1, i]+self.dt*self.grid[-1, i+1] )
            
            Ux = sla.solve_triangular( M_lower, Q, lower=True )
            self.grid[1:-1, i] = sla.solve_triangular( M_upper, Ux, lower=False )
            
    def _interpolate_(self):
        tck = spi.splrep( self.Svec, self.grid[:,0], k=3 )
        return spi.splev( self.St, tck )
    
    def price(self):
        self._set_terminal_condition_()
        self._set_boundary_condition_()
        self._set_coefficient_()
        self._solve_()
        return self._interpolate_()*self.Principal

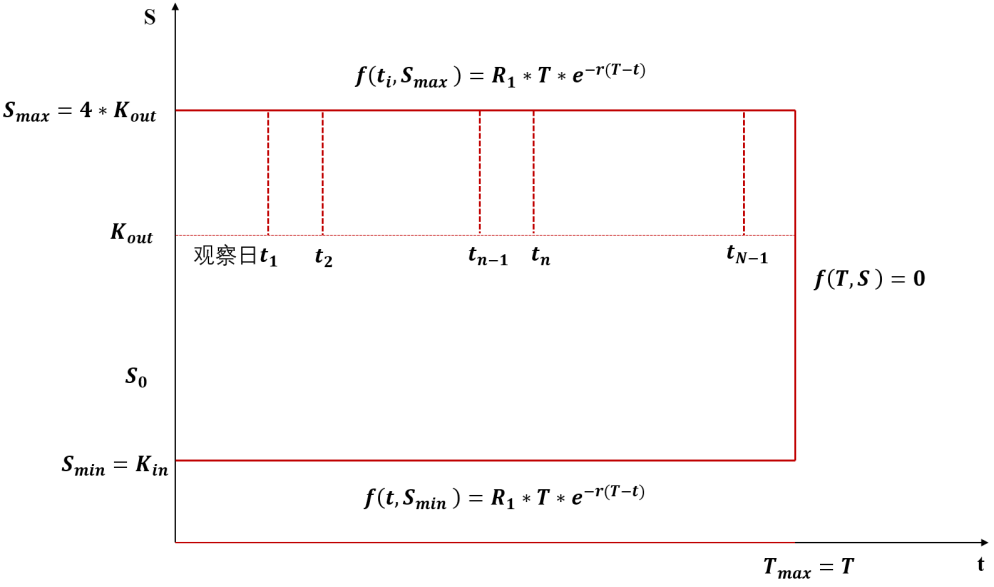
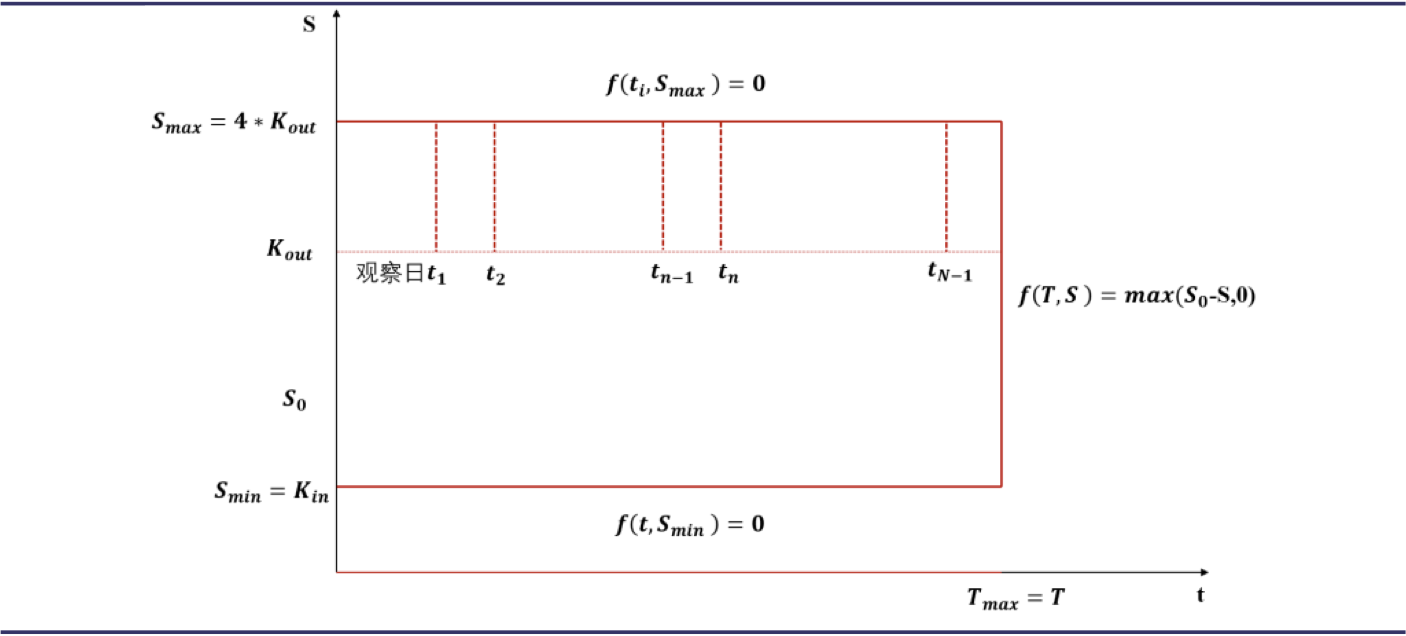
情景2: 未敲入未敲出

若标的价格一直在敲入价 $K{in}$ 和敲出价 $K{out}$ 范围内，即未触碰上下边界，则产品期末有收益率 = $c_1$ 。这种情况下的支付可看作一个双边失效触碰期权（Double No-Touch，DNT）。

$\begin{equation} V_2 = \text{DNT}(R=c_2) \end{equation}$

其中 $R_1$ 是红利票息

首先我们定义双边触碰生效期权（Double One-Touch，DOT），DOT 与 DNT 支付结构对称，当标的价格触碰到敲出价时才进行支付，否则支付为 0。因此，一个双边触碰失效期权（DNT）与双边触碰生效期权（DOT）的组合是无风险的，在期末获得无风险收益 $R_1$ 。两者价格存在如下平价关系：

$DNT +DOT = c_2 T \exp\{-rT\}$

双边触碰生效期权（DOT）PDE 示意图

class Snowball_Double_No_Touch(Snowball_Parameters):
    """
    present value of bonus coupon if not KO and not KI
    V_{DNT}+V_{DOT} = R * exp{-r*T}
    """
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.Smax = 4 * self.KO_price
        self.Smin = self.KI_price
        self.dS =  (self.Smax-self.Smin)/self.Ns
        self.Svec = np.linspace(self.Smin, self.Smax, self.Ns+1)
        self.grid = np.zeros(shape=(self.Ns+1, self.Nt+1))
        self.Return = self.T * self.Bonus_Coupon
          
    def _set_terminal_condition_(self):
        pass
    
    def _set_boundary_condition_(self):
        # upper bound at non-knock-out point
        self.grid[0,  :] = self.Return * np.exp(-self.r* self.tau)
        self.grid[-1,  :] = self.Return * np.exp(-self.r* self.tau)
    
    def _set_coefficient_(self):
        drift = (self.r-self.div)*self.Svec[1:-1]/self.dS
        diffusion_square = (self.sigma*self.Svec[1:-1]/self.dS)**2
        
        self.l = 1/4*(diffusion_square - drift)
        self.c = 1/2*(-diffusion_square - self.r)
        self.u = 1/4*(diffusion_square + drift)

        self.A = sp.diags([self.l[1:], self.c, self.u[:-1]], [-1, 0, 1],  format='csc')
        self.I = sp.eye(self.Ns-1)
        self.M1 = self.I - self.dt*self.A
        self.M2 = self.I + self.dt*self.A
        
    def _solve_(self):
        _, M_lower, M_upper = sla.lu(self.M1.toarray())
        
        #* 1.set boundary condition at T_KO
        KO_idx = np.searchsorted(self.Tvec, self.T_KO)
        update_bool_idx =  (self.Svec>=self.KO_price)
        rbt = self.Return * np.exp(-self.r*(self.T-self.T_KO)) #! set boundary condition at T_KO
        for i in reversed(np.arange(self.Nt)):
            #* 2.set boundary condition at T_KO
            if i+1 in KO_idx:
                k = np.where(KO_idx==i+1)[0]
                self.grid[update_bool_idx, i+1] = rbt[k]  

            Q = self.M2.dot(self.grid[1:-1, i+1])
            
            Q[0] += self.l[0]*(self.dt*self.grid[0, i] +self.dt*self.grid[0, i+1] )
            Q[-1] += self.u[-1]*(self.dt*self.grid[-1, i]+self.dt*self.grid[-1, i+1] )
            
            Ux = sla.solve_triangular( M_lower, Q, lower=True )
            self.grid[1:-1, i] = sla.solve_triangular( M_upper, Ux, lower=False )
            
    def _interpolate_(self):
        tck = spi.splrep( self.Svec, self.grid[:,0], k=3 )
        return spi.splev( self.St, tck )
    
    def price(self):
        self._set_terminal_condition_()
        self._set_boundary_condition_()
        self._set_coefficient_()
        self._solve_()
        V_DOT = self._interpolate_()
        V_R = (self.Return) * np.exp(-self.r*self.T)
        return  (V_R - V_DOT) * self.Principal

情景3: 敲入未敲出

put short 卖一个看跌期权

情景三下的支付就是卖一个本金为 $\frac{1}{S_0}$，行权价格为期初价格 $K=S_0$ 的看跌期权 (注意负号)，收益率 = $-\frac{1}{S_0}\text{max}\left(K-S_T, 0\right)$

敲入未敲出——保本

\
敲入未敲出——亏本

情景三的支付可由一个上涨失效看跌障碍期权 (Up and Out Put, UOP) 和一个双边失效看跌障碍期权 (Double Knock-Out Put, DKOP) 来复制

$\begin{equation} V_3 = \frac{1}{S_0}\times[\text{DKOP}(K=S_0,K_{in},K_{out}) - \text{UOP}(K=S_0,K_{out})] \end{equation}$

其中 $\frac{1}{S_0}$ 是 UOP 和 DKOP 的本金。

验证“情景三的支付”和“复制组合的支付”是否一致，先看 $V_3$ 的支付情况：

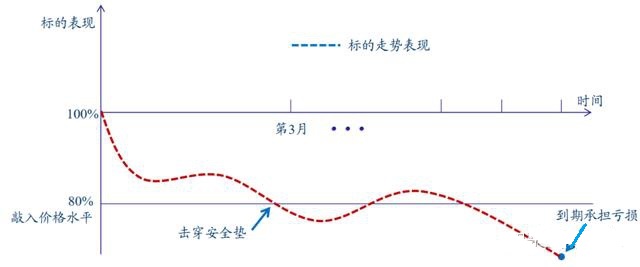
情景一：只要敲出 (不管是否敲入)，支付为零
情景二：既没敲入也没敲出，支付为零
情景三：但只要敲入而且从未敲出时，到期日支付为 $-\frac{1}{S_0}\text{max}\left(K-S_T, 0\right)$

再看 DKOP - UOP 的支付情况：

情景一：只要敲出，UOP 和 DKOP 都敲出，两个支付都为零，因此总支付为零，吻合
情景二：既没敲入也没敲出，UOP 和 DKOP 到期日的支付一样，两者相减总支付为零，吻合
情景三：当价格触碰 DKOP 下边界但没有触碰上边界时，DKOP 敲出支付为零，UOP 保持看跌期权的支付 $\text{max}(S_0 - S_T, 0)$，带着本金两者相减总支付 $-\frac{1}{S_0}\text{max}(S_0 - S_T, 0)$，吻合

class Snowball_Up_Out_Put(Snowball_Parameters):   
    '''
    value of up out put
    '''
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.Smax = 4 * self.S      #? K_out?
        self.Smin = 0
        self.dS =  (self.Smax-self.Smin)/self.Ns
        self.Svec = np.linspace(self.Smin, self.Smax, self.Ns+1)
        self.grid = np.zeros(shape=(self.Ns+1, self.Nt+1))
        self.Return = 0 #!UOP f=0 at (T_KO, which >KO_price)

    def _set_terminal_condition_(self):
        self.grid[:, -1] = np.maximum((self.S - self.Svec ), 0)
    
    def _set_boundary_condition_(self):
        DF_div = np.exp(-self.div*self.tau)
        DF_r = np.exp(-self.r*self.tau)

        self.grid[0,  :] = np.maximum(self.S * DF_r - self.Smin * DF_div, 0) #! S_0 * DF
        # self.grid[0,  :] = self.S * np.exp(-self.r*self.tau)
        self.grid[-1, :] = 0 

    def _set_coefficient_(self):
        drift = (self.r-self.div)*self.Svec[1:-1]/self.dS
        diffusion_square = (self.sigma*self.Svec[1:-1]/self.dS)**2
        
        self.l = 1/4*(diffusion_square - drift)
        self.c = 1/2*(-diffusion_square - self.r)
        self.u = 1/4*(diffusion_square + drift)

        self.A = sp.diags([self.l[1:], self.c, self.u[:-1]], [-1, 0, 1],  format='csc')
        self.I = sp.eye(self.Ns-1)
        self.M1 = self.I - self.dt*self.A
        self.M2 = self.I + self.dt*self.A

    def _solve_(self):
        _, M_lower, M_upper = sla.lu(self.M1.toarray())
        #* 1.set boundary condition at T_KO
        KO_idx = np.searchsorted(self.Tvec, self.T_KO)
        update_bool_idx =  (self.Svec>=self.KO_price)
        rbt = self.Return * np.exp(-self.r*(self.T-self.T_KO)) #* note that self.Return = 0
        for i in reversed(np.arange(self.Nt)):
            #* 2.set boundary condition at T_KO
            if i+1 in KO_idx:
                k = np.where(KO_idx==i+1)[0]
                self.grid[update_bool_idx, i+1] = rbt[k]  

            Q = self.M2.dot(self.grid[1:-1, i+1])
            
            Q[0] += self.l[0]*(self.dt*self.grid[0, i] +self.dt*self.grid[0, i+1] )
            Q[-1] += self.u[-1]*(self.dt*self.grid[-1, i]+self.dt*self.grid[-1, i+1] )
            
            Ux = sla.solve_triangular( M_lower, Q, lower=True )
            self.grid[1:-1, i] = sla.solve_triangular( M_upper, Ux, lower=False )
            
    def _interpolate_(self):
        tck = spi.splrep( self.Svec, self.grid[:,0], k=3 )
        return spi.splev( self.St, tck )
    
    def price(self):
        self._set_terminal_condition_()
        self._set_boundary_condition_()
        self._set_coefficient_()
        self._solve_()
        return self._interpolate_()/self.S * self.Principal


class Snowball_Double_Knock_Out_Put(Snowball_Parameters):   
    '''
    value of double konck-out put
    '''
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.Smax = 4 * self.S      #? K_out?
        self.Smin = self.KI_price
        self.dS =  (self.Smax-self.Smin)/self.Ns
        self.Svec = np.linspace(self.Smin, self.Smax, self.Ns+1)
        self.grid = np.zeros(shape=(self.Ns+1, self.Nt+1))
        self.Return = 0 #!UOP f=0 at (T_KO, which >KO_price)

    def _set_terminal_condition_(self):
        self.grid[:, -1] = np.maximum((self.S - self.Svec ), 0)
    
    def _set_boundary_condition_(self):
        self.grid[0,  :] = 0
        self.grid[-1, :] = 0


    def _set_coefficient_(self):
        drift = (self.r-self.div)*self.Svec[1:-1]/self.dS
        diffusion_square = (self.sigma*self.Svec[1:-1]/self.dS)**2
        
        self.l = 1/4*(diffusion_square - drift)
        self.c = 1/2*(-diffusion_square - self.r)
        self.u = 1/4*(diffusion_square + drift)

        self.A = sp.diags([self.l[1:], self.c, self.u[:-1]], [-1, 0, 1],  format='csc')
        self.I = sp.eye(self.Ns-1)
        self.M1 = self.I - self.dt*self.A
        self.M2 = self.I + self.dt*self.A

    def _solve_(self):
        _, M_lower, M_upper = sla.lu(self.M1.toarray())
        #* 1.set boundary condition at T_KO
        KO_idx = np.searchsorted(self.Tvec, self.T_KO)
        update_bool_idx =  (self.Svec>=self.KO_price)
        rbt = self.Return * np.exp(-self.r*(self.T-self.T_KO)) #* note that self.Return = 0
        for i in reversed(np.arange(self.Nt)):
            #* 2.set boundary condition at T_KO
            if i+1 in KO_idx:
                k = np.where(KO_idx==i+1)[0]
                self.grid[update_bool_idx, i+1] = rbt[k]  

            Q = self.M2.dot(self.grid[1:-1, i+1])
            
            Q[0] += self.l[0]*(self.dt*self.grid[0, i] +self.dt*self.grid[0, i+1] )
            Q[-1] += self.u[-1]*(self.dt*self.grid[-1, i]+self.dt*self.grid[-1, i+1] )
            
            Ux = sla.solve_triangular( M_lower, Q, lower=True )
            self.grid[1:-1, i] = sla.solve_triangular( M_upper, Ux, lower=False )
            
    def _interpolate_(self):
        tck = spi.splrep( self.Svec, self.grid[:,0], k=3 )
        return spi.splev( self.St, tck )
    
    def price(self):
        self._set_terminal_condition_()
        self._set_boundary_condition_()
        self._set_coefficient_()
        self._solve_()
        return self._interpolate_()/self.S * self.Principal

定价雪球

class Snowball(Snowball_Parameters):
    '''
    计算雪球期权的价格
    '''
    def __init__(self, **kwargs):
        super().__init__(**kwargs)

        
    def compute_price(self, **kwargs):
        default_kwargs = self.__dict__.copy()
        default_kwargs.update(kwargs)
        case1 = Snowball_One_Touch_Up(**default_kwargs)
        case2 = Snowball_Double_No_Touch(**default_kwargs)
        case3_1 = Snowball_Up_Out_Put(**default_kwargs)
        case3_2 = Snowball_Double_Knock_Out_Put(**default_kwargs)
        
        # print("Computing prices for different cases:")
        
        V1 = case1.price()
        # print("1. Knock-out: {:.2f}".format(V1))
        
        V2 = case2.price()
        # print("2. Not knock-out and not knock-in: {:.2f}".format(V2))
        
        V3 = case3_2.price() - case3_1.price()
        # print("3. Not knock-out and knock-in: {:.2f}".format(V3))
        
        V = V1 + V2 + V3
        # print("---------------------------------------------")
        # print("Option price: {:.2f}".format(V))
        self.P = {"V":[V, V1, V2, V3],"grid":[case1.grid,case2.grid,case3_1.grid,case3_2.grid]
               ,"Svec":[case1.Svec,case2.Svec,case3_1.Svec,case3_2.Svec]}
        return self.P
    
    
    def greeks_vega(self):
        #! 需要mid吗，还是+1
        epsilon = 0.01
#         P_base = self.compute_price()[0]
        P_vega1 = self.compute_price(sigma = self.sigma+epsilon)['V'][0]
        P_vega2 = self.compute_price(sigma = self.sigma-epsilon)['V'][0]
        
        return  (P_vega2 - P_vega1) / (2*epsilon*self.Principal)
    
    def interpolate(self,Svec,grid,S,J):
        tck = spi.splrep( Svec, grid[:,J], k=3 )
        return spi.splev( S, tck )
    
    def greeks_delta(self, percentile=1, J=0):
        epsilon = 0.01
        # P = self.compute_price(sigma = self.sigma)
        
        P_base_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile,J )
        P_base_2 =  self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  - self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile,J ) 
        P_base_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile,J )/(self.S * percentile)
        P_base_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile,J )/(self.S * percentile)
        P_base = P_base_1 +  P_base_2 - P_base_3 + P_base_4

        
        P1_delta_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile *(1 + epsilon),J)
        P1_delta_2 = self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  - self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile *(1 + epsilon),J)
        P1_delta_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile *(1 + epsilon),J)/(self.S * percentile *(1 + epsilon))
        P1_delta_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile *(1 + epsilon),J)/(self.S * percentile *(1 + epsilon))
        P1_delta = P1_delta_1 + P1_delta_2 - P1_delta_3 + P1_delta_4

        P2_delta_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile *(1 - epsilon),J)
        P2_delta_2 = self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  -self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile *(1 - epsilon),J)
        P2_delta_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile *(1 - epsilon),J)/(self.S * percentile *(1 - epsilon))
        P2_delta_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile *(1 - epsilon),J)/(self.S * percentile *(1 - epsilon))
        P2_delta = P2_delta_1 + P2_delta_2 - P2_delta_3 + P2_delta_4

        delta1 = self.Principal * (P1_delta - P2_delta) / (2 * self.S * percentile * epsilon) #* self.S * percentile
        delta2 =  (P1_delta - P2_delta) / (2 * self.S * percentile * epsilon) * self.S * percentile
        # gamma = (P1_delta + P2_delta - 2 * P_base) / ((self.S * percentile) **2 * epsilon**2)
        return (delta1,delta2)

该雪球结构期权的定价公式如下：

$\begin{align*} V_{\text{snowball}} &= V_1 + V_2 + V_3 \\ & = \text{OTU}\left(R=\left[\frac{3c_1\%}{12},\frac{4c_1\%}{12},\cdots,\frac{12c_1\%}{12}\right]\right) \\ & + \text{DNT}(R=c_2\%) \\ & + \frac{1}{S_0}\times[\text{DKOP}(K=S_0,K_{out},K_{in}) - \text{UOP}(K=S_0,K_{out})] \end{align*}$

(Principal,S,T,KI_Barrier,KO_Barrier,KO_Coupon,Bonus_Coupon) = (10**6,6500,1,0.8,1.03,0.25,0.25)
T_KO = np.arange(30*3/360,30*12.1/360,30/360)  #* 这里选12.1是因为最后一天是360/365
(r, div, sigma) = (0.03, 0, 0.2455)
(Ns, Nt) = (500, int(np.ceil(T*360) ) ) #! 分成多少份365，还是360

pde = Snowball(Principal = Principal,T = T, S = S, St = 6500, KI_Barrier = KI_Barrier, KO_Barrier = KO_Barrier, KO_Coupon = KO_Coupon, Bonus_Coupon = Bonus_Coupon, r= r, div = div, sigma = sigma, Ns = Ns, Nt = Nt, T_KO = T_KO)
pde.print_parameters()
tic = time.time()
# print("Computing prices for different cases:")
print("Option price: {:.2f}".format(pde.compute_price()['V'][0]))
print( "---------------------------------------------" )

---------------------------------------------
Pricing a Snowball option using PDE
---------------------------------------------
Parameters of Snowball Option Pricer:
---------------------------------------------
Years Until Expiration =  1
Principal =  1000000
Underlying Asset Price =  6500
Knock-in Barrier =  0.8
Autocall Barrier =  1.03
Knock-in Price =  5200.0
Autocall Price =  6695.0
Autocall Coupon =  0.25
Bonus Coupon =  0.25
Risk-Free Rate = 0.03
Dividend Rate = 0
Volatility =  0.2455
Discrete underlying points = 500
Discrete time points = 360
Time-Step =  0.002777777777777778
Knock-in Price =  5200.0
Knock-out Price =  6695.0
Knock out time =  [0.25       0.33333333 0.41666667 0.5        0.58333333 0.66666667
 0.75       0.83333333 0.91666667 1.        ]
---------------------------------------------
Option price: 20390.14
---------------------------------------------

Delta分析

不同波动率对应的delta曲面

计算公式:

$Delta = \frac{f(S_0+\Delta S)-f(S_0-\Delta S)}{2\Delta S/S_0}$

其中 $\Delta S = 0.01 \times S_0$

波动率曲面：选取雪球发行日当天，观察不同波动率条件下（0.1-0.45），雪球Greeks在不同资产价格的变动情况。波动率越低，Delta在敲入与敲出水平线附近变动越剧烈，以上图为例，波动率为10%时，Delta在敲入水平处高达4.77，在敲出水平最低达到-0.92


price_set = np.linspace(0.8 ,1.3, 50)
sigma_set = np.linspace(0.1 , 0.45, 20)

price_set_,sigma_set_ = np.meshgrid(price_set,sigma_set )
option_set1 = np.zeros_like(sigma_set_)
option_set2 = np.zeros_like(sigma_set_)

for idx,sigma in enumerate(sigma_set):
    pde = Snowball(sigma = sigma)
    pde.compute_price()
    for idx_,per in enumerate(price_set):
        option_set1[idx,idx_] = pde.greeks_delta(per,0)[0]
        option_set2[idx,idx_] = pde.greeks_delta(per,0)[1]

surface = go.Surface(x=price_set_, y=sigma_set_, z=option_set1)
fig = go.Figure(data=[surface])
fig.update_layout(
    scene=dict(
        aspectmode='cube',
        xaxis_title='Price',
        yaxis_title='Sigma',
        zaxis_title='Delta'
    ),
    title='Delta surfaces corresponding to different volatility at start-date',
        width=800,  
    height=600  
)
fig.update_traces(opacity=0.7)
fig.show()

surface = go.Surface(x=price_set_, y=sigma_set_, z=option_set2)
fig = go.Figure(data=[surface])
fig.update_layout(
    scene=dict(
        aspectmode='cube',
        xaxis_title='Price',
        yaxis_title='Sigma',
        zaxis_title='Delta'
    ),
    title='Delta surfaces corresponding to different volatility at start-date',
        width=800,  
    height=600  
)
fig.update_traces(opacity=0.7)
fig.show()

不同日期下对应的delta曲面

price_set = np.linspace(0.8 ,1.3, 50)
Nt_set = np.linspace(0,Nt,Nt+1)

price_set_,Nt_set_ = np.meshgrid(price_set,Nt_set )
option_set = np.zeros_like(Nt_set_)

pde = Snowball(sigma = 0.2)
pde.compute_price()

for idx,t in enumerate(Nt_set):
    for idx_,per in enumerate(price_set):
        option_set[idx,idx_] = pde.greeks_delta(per,idx)[0]

surface = go.Surface(x=price_set_, y=Nt_set_, z=option_set)
fig = go.Figure(data=[surface])
fig.update_layout(
    scene=dict(
        aspectmode='cube',
        xaxis_title='Price',
        yaxis_title='Nt',
        zaxis_title='Delta'
    ),
    title='Delta surfaces corresponding to different date at sigma = 0.2',
        width=800,  
    height=600  
)
fig.update_traces(opacity=0.7)
fig.show()

Gamma分析

计算公式:

$\Gamma = \frac{f^\prime(S_0+\Delta S)-f^\prime(S_0-\Delta S)}{2\Delta S/S_0}$

其中$\Delta S = 0.01 \times S_0$。

class Snowball(Snowball_Parameters):
    '''
    计算雪球期权的价格
    '''
    def __init__(self, **kwargs):
        super().__init__(**kwargs)

        
    def compute_price(self, **kwargs):
        default_kwargs = self.__dict__.copy()
        default_kwargs.update(kwargs)
        case1 = Snowball_One_Touch_Up(**default_kwargs)
        case2 = Snowball_Double_No_Touch(**default_kwargs)
        case3_1 = Snowball_Up_Out_Put(**default_kwargs)
        case3_2 = Snowball_Double_Knock_Out_Put(**default_kwargs)
        
        # print("Computing prices for different cases:")
        
        V1 = case1.price()
        # print("1. Knock-out: {:.2f}".format(V1))
        
        V2 = case2.price()
        # print("2. Not knock-out and not knock-in: {:.2f}".format(V2))
        
        V3 = case3_2.price() - case3_1.price()
        # print("3. Not knock-out and knock-in: {:.2f}".format(V3))
        
        V = V1 + V2 + V3
        # print("---------------------------------------------")
        # print("Option price: {:.2f}".format(V))
        self.P = {"V":[V, V1, V2, V3],"grid":[case1.grid,case2.grid,case3_1.grid,case3_2.grid]
               ,"Svec":[case1.Svec,case2.Svec,case3_1.Svec,case3_2.Svec]}
        return self.P
    
    
    def greeks_vega(self):
        #! 需要mid吗，还是+1
        epsilon = 0.01
#         P_base = self.compute_price()[0]
        P_vega1 = self.compute_price(sigma = self.sigma+epsilon)['V'][0]
        P_vega2 = self.compute_price(sigma = self.sigma-epsilon)['V'][0]
        
        return  (P_vega2 - P_vega1) / (2*epsilon*self.Principal)
    
    def interpolate(self,Svec,grid,S,J):
        tck = spi.splrep( Svec, grid[:,J], k=3 )
        return spi.splev( S, tck )
    
    def greeks_delta(self, percentile, J):
        epsilon = 0.01
        # P = self.compute_price(sigma = self.sigma)
        
        P_base_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile,J )
        P_base_2 =  self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  - self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile,J ) 
        P_base_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile,J )/(self.S * percentile)
        P_base_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile,J )/(self.S * percentile)
        P_base = P_base_1 +  P_base_2 - P_base_3 + P_base_4

        
        P1_delta_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile *(1 + epsilon),J)
        P1_delta_2 = self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  - self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile *(1 + epsilon),J)
        P1_delta_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile *(1 + epsilon),J)/(self.S * percentile *(1 + epsilon))
        P1_delta_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile *(1 + epsilon),J)/(self.S * percentile *(1 + epsilon))
        P1_delta = P1_delta_1 + P1_delta_2 - P1_delta_3 + P1_delta_4

        P2_delta_1 = self.interpolate(self.P['Svec'][0],self.P['grid'][0],self.S * percentile *(1 - epsilon),J)
        P2_delta_2 = self.T * self.Bonus_Coupon * np.exp(-self.r*self.T)  -self.interpolate(self.P['Svec'][1],self.P['grid'][1],self.S * percentile *(1 - epsilon),J)
        P2_delta_3 = self.interpolate(self.P['Svec'][2],self.P['grid'][2],self.S * percentile *(1 - epsilon),J)/(self.S * percentile *(1 - epsilon))
        P2_delta_4 = self.interpolate(self.P['Svec'][3],self.P['grid'][3],self.S * percentile *(1 - epsilon),J)/(self.S * percentile *(1 - epsilon))
        P2_delta = P2_delta_1 + P2_delta_2 - P2_delta_3 + P2_delta_4

        delta = (P1_delta - P2_delta) / (2 * self.S * percentile * epsilon) * self.S * percentile
        gamma = (P1_delta + P2_delta - 2 * P_base) / ((self.S * percentile) **2 * epsilon**2)
        return (delta,gamma)